La matriz Hessiana es una matriz cuadrada de derivadas parciales de segundo orden de una función con valores escalares, o campo escalar. Describe la curvatura local de una función de muchas variables.

Basicamente la matriz Hessiana es una herramienta matemática que se utiliza para calcular la curvatura de una función en un determinado punto del espacio. Esta matriz juega un papel importante en muchos algoritmos de aprendizaje automático, que implica la optimización de una función determinada. El hessiano no es más que el gradiente del gradiente, una matriz de segundas derivadas parciales.

¿Qué es la optimización de una función?

Las derivadas de segundo orden se utilizan para tener una idea de la forma de la gráfica de la función dada. Si será de arriba a abajo. Se basa en la concavidad. La concavidad de la función gráfica dada se clasifica en dos tipos: Cóncava hacia arriba y Cóncava hacia abajo.

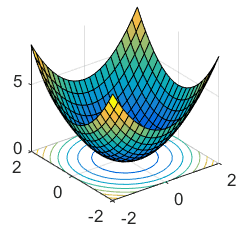
Cóncava hacia arriba: Una función es cóncava si su curvatura es hacia abajo, es decir, si la función está curvada hacia abajo en un intervalo dado. Para determinar la concavidad de una función utilizando derivadas de segundo orden, se observa el signo de la segunda derivada. Si la segunda derivada es negativa en un punto, entonces la función es cóncava en ese punto.

Cóncava hacia abajo: Por otro lado, una función es convexa si su curvatura es hacia arriba, es decir, si la función está curvada hacia arriba en un intervalo dado. Para determinar la convexidad de una función utilizando derivadas de segundo orden, se observa el signo de la segunda derivada. Si la segunda derivada es positiva en un punto, entonces la función es convexa en ese punto.

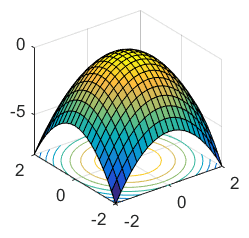
Debo aclarar algo: la matriz Hessiana describe la curvatura de una función en un punto dado, pero no todas las funciones tienen una representación gráfica simple en un plano 3D. Algunas funciones pueden tener una dimensión mayor, lo que significa que la matriz Hessiana sería más grande que una matriz 3×3, lo cual no es compatible con una representación gráfica en un plano 3D.

¿Cuales son sus usos en Machine Learning?

1. 1. Optimización de funciones: En muchos algoritmos de aprendizaje automático, como los utilizados en el entrenamiento de redes neuronales, se busca minimizar una función de costo para ajustar los parámetros del modelo. La matriz Hessiana puede proporcionar información sobre la curvatura de esta función de costo en el espacio de parámetros, lo que puede ser útil para elegir algoritmos de optimización adecuados y ajustar sus hiperparámetros para mejorar la convergencia y la eficiencia del entrenamiento.

2. 2. Newton-Raphson y métodos de segundo orden: Algunos algoritmos de optimización de segundo orden, como el método de Newton-Raphson, utilizan información del Hessiano para determinar la dirección y la longitud de los pasos de búsqueda durante el entrenamiento. Estos métodos pueden converger más rápidamente hacia el óptimo que los métodos de primer orden, como el descenso de gradiente, especialmente en problemas donde la función de costo es altamente no lineal o no convexa.

3. 3. Diagnóstico de convergencia: El análisis del Hessiano durante el entrenamiento puede proporcionar información sobre la convergencia del algoritmo de optimización y la estabilidad del modelo. Por ejemplo, cambios bruscos en los valores propios del Hessiano pueden indicar problemas de convergencia o inestabilidad numérica durante el entrenamiento.

4. 4. Regularización y prevención de sobreajuste: El Hessiano también se puede utilizar para calcular la información de Fisher, que es útil en técnicas de regularización como la regularización de Tikhonov (ridge) o la regularización de Laplace (L1), así como para prevenir el sobreajuste y mejorar la generalización del modelo.

¿Que es el discriminante de una matriz Hessiana?

El discriminante de la matriz Hessiana, tambien conocido como determinante, es útil para determinar la naturaleza de un punto crítico. La matriz Hessiana proporciona información sobre la curvatura de la función en un punto dado, y su discriminante (el valor que resulta de calcular el determinante de la matriz Hessiana) es una cantidad importante para clasificar los puntos críticos:

1. 1. Si el discriminante es positivo y todos los autovalores son positivos, entonces el punto crítico es un mínimo local.

2. 2. Si el discriminante es positivo y todos los autovalores son negativos, entonces el punto crítico es un máximo local.

3. 3. Si el discriminante es negativo, entonces el punto crítico es un punto de silla.

Para una función de dos variables f(x, y), la fórmula para calcular su valor determinante es la siguiente:

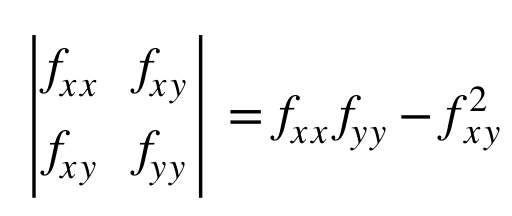
Veámoslo con un ejemplo. Supongamos que tenemos la siguiente función:

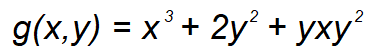
Calculamos su primera derivada y luego calculamos su Hessiano. Una vez calculado el Hessiano, lo usamos para calcular el determinante de acuerdo a la fórmula que tenemos más arriba:

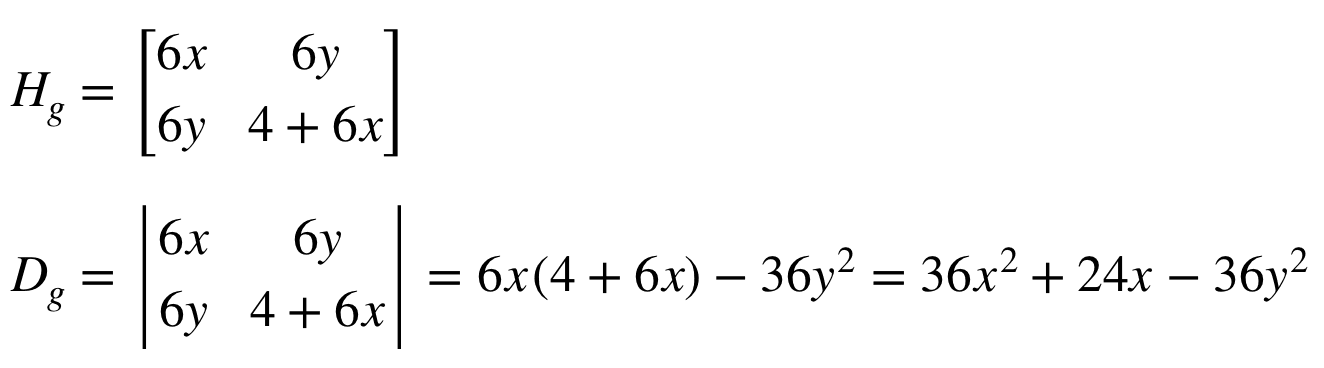
Evaluemos los discriminantes en diferentes puntos:

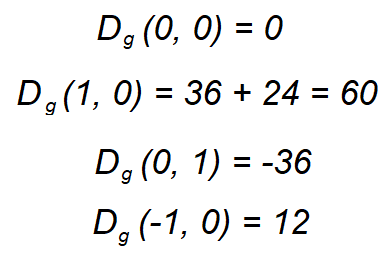
¿Que son los autovalores de una matriz Hessiana?

Los autovalores de una matriz representan las escalas por las cuales los vectores se expanden o contraen cuando se aplica esa matriz como una transformación lineal. En otras palabras, los autovalores nos dicen cómo la matriz estira o encoge los vectores en diferentes direcciones. Los autovalores se calculan de la siguiente manera:

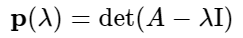
Siendo A una matriz cualquiera e I su respectiva matriz identidad en este caso mostraremos una matriz de 2x2, pero el ejemplo se puede dar con matrices de mayor tamaño:

¿Qué es una matriz identidad?

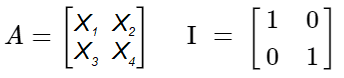
Veámoslo con un ejemplo. Supongamos que tenemos una matriz A de 2x2 con su respectiva matriz de identidad y queremos calcular sus autovalores.

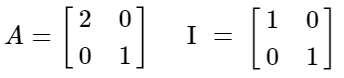
Planteamos la ecuación para obtener los autovalores que aprendimos anteriormente:

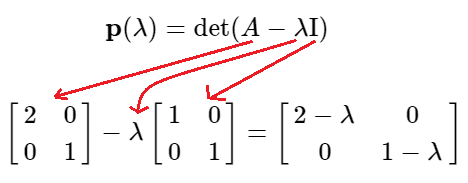
Luego planteamos el determinante de la matriz resultante y lo igualamos a cero para encontrar las raíces de esa función:

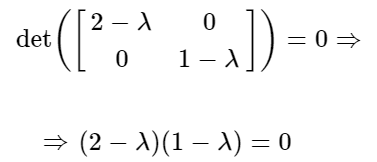
Esto nos indica que las raíces son λ=2 y λ=1.

¿Como se usa la matriz hessiana para optimizar una función?

Al momento de optimizar una función de recompensa en inteligencia artificial podemos estimar la función y su gradiente (cómo cambiar x para mejorar y) usando primeras derivadas. Las segundas derivadas nos ayudan a identificar la dirección en la que debemos movernos para minimizar la función. Estas figuras representan cómo cambia la función para cada incremento de x, en el punto x. Este método requiere una modificación cuando se aplica a un problema con múltiples dimensiones, como el modelado de imágenes, porque la entrada a la función ya no es un punto único sino un vector.

Para trabajar con problemas de optimización multivariante, tomamos la matriz jacobiana y la convertimos en una matriz de Hesse tomando las derivadas de segundo orden de cada vector. Este escenario requiere nueva información ya que existe una segunda derivada diferente para un solo punto en cada dirección posible; los valores propios producidos representan el cambio en cada dirección. La segunda derivada representa el valor propio o cómo podemos esperar que se realice el descenso del gradiente en esa dirección. El método de Newton (búsqueda de líneas) se utiliza para determinar los pasos que debe seguir el descenso del gradiente para minimizar la función.

Cuando digo que la función objetivo es multivariante, quiero decir que la recompensa esperada depende de múltiples parámetros de la política. Estos parámetros podrían ser los pesos de una red neuronal, y la función objetivo (la recompensa esperada) es una función de estos pesos, lo que hace que sea una función multivariante. La optimización implica encontrar los valores óptimos de estos parámetros para maximizar la recompensa esperada.

Ejemplos

Consideremos otra función 'f(x, y)', su primera derivada 'J' y su matriz Hessiana 'H':

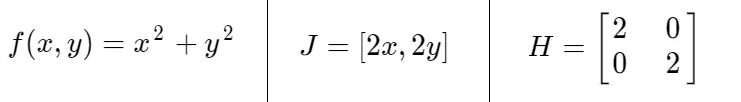
Si se grafica la función f(x, y) y se la mirara desde arriba hacia abajo e isométricamente se vería así:

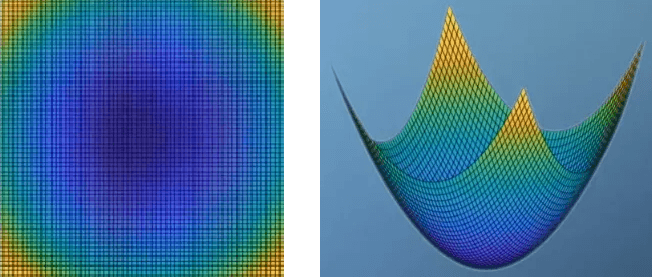
Ahora digamos que no habías visto la función de antemano y calculaste el valor del jacobiano en el punto (0,0). Verás que el vector gradiente también era 0, pero ¿cómo sabrías si era un máximo o un mínimo en ese punto? Simplemente podemos mirar el Hessiano, y si tuviéramos que resolver el determinante del Hessiano obtendríamos:

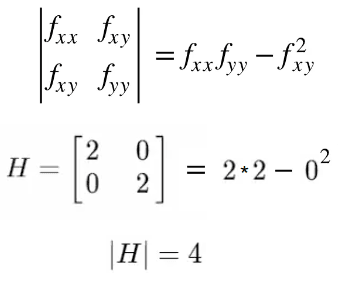
Esta informacion es util pero no es suficiente para sacar conclusiones sobre si ese punto es un maximo o minimo local. Debemos calcular los autovalores para saber esto. Entonces planteamos la ecuacion para obtener los autovalores:

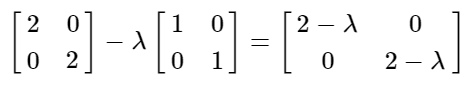
Luego planteamos el determinante de la ecuacion y lo resolvemos:

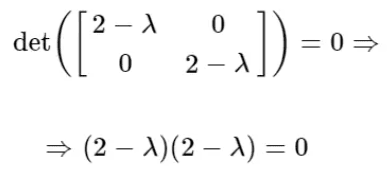
Ahora sabemos que las raices son λ=2 y λ=2. Dado que tenemos los autovalores y el determinante, podemos evaluar si el el punto es un minimo o maximo local de acuerdo a las condiciones que hay mas arriba:

1. 1. Si el discriminante es positivo y todos los autovalores son positivos, entonces el punto crítico es un mínimo local. En mi caso si es cierto, ya que los autovalores son λ=2 y λ=2 y el discriminante es 4, todos son valores positivos ✔️.

2. 2. Si el discriminante es positivo y todos los autovalores son negativos, entonces el punto crítico es un máximo local. En mi caso no es cierto, ya que los autovalores son positivos ❌.

3. 2. Si el discriminante es negativo, entonces el punto crítico es un punto de silla. En mi caso no es cierto porque el discriminante es positivo ❌.

Dicho esto, podemos decir que el punto (0,0) es un minimo local.

Por ultimo debo aclarar que en ciertos casos, es posible que puntos cercanos a un mínimo local también sean mínimos locales, especialmente si la función es suave y tiene un comportamiento regular en su vecindario. Por ejemplo, si una función tiene un mínimo local en un punto (0,0) y es continua y suave en un entorno de este punto, es posible que exista un conjunto de puntos cercanos a (0,0), como por ejemplo (0,1), que también sean mínimos locales.

Conclusiones

La matriz Hessiana es una herramienta valiosa en el contexto del machine learning, especialmente en problemas de optimización asociados con el entrenamiento de modelos de aprendizaje automático. Proporciona información sobre la curvatura de las funciones objetivo y puede ser utilizada para mejorar la convergencia, la estabilidad y la generalización de los modelos entrenados.

Hemos llegado al final de este artículo. Espero que te halla resultado útil y que hallas disfrutado leyéndolo tanto como yo disfrute escribiéndolo 😁.