El gradiente o tambien conocido como vector gradiente​ de un campo escalar $f:\R\rightarrow\R^n$ es un campo vectorial, denotado como $∇f$. El vector gradiente de $f$ evaluado en un punto genérico $x$ del dominio de $f$ indica la dirección en la cual el campo $f$ varía más rápidamente y su módulo representa el ritmo de variación de $f$ en la dirección de dicho vector gradiente.

¿Qué es un campo escalar y campo vectorial?

Para que lo veas de una manera más grafica en la siguiente imagen se puede observar un plano cuadriculado en el cual existe un campo escalar, donde cada punto de dicho plano tiene asignado un vector con su respectiva magnitud y dirección:

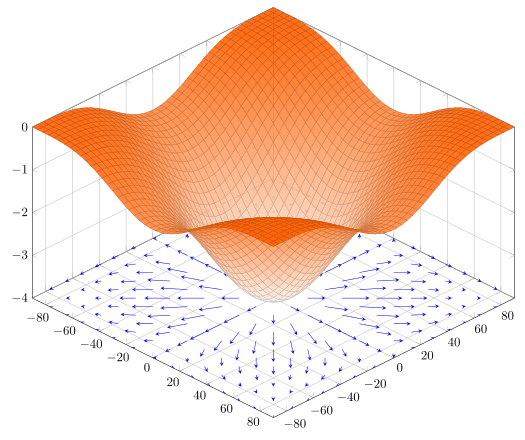
Pero no son magnitudes y direcciones aleatorias, sino que cumplen las dos siguientes propiedades:

1. 
   1. La magnitud es proporcional a la pendiente: Es decir que mientras mayor sea el cambio, mayor será la magnitud del gradiente. En la imagen de la izquierda se puede apreciar que no todos los gradientes tienen la misma magnitud, sino que existen algunos más pequeños y otros más grandes. Todos los gradientes dentro del perímetro delimitado por la línea roja son los que podríamos considerar los más grandes. Al ser los más grandes significa que su pendiente es más pronunciada, lo que podemos confirmar por el gráfico de la función naranja que está arriba. Podemos comparar la forma del gráfico con las posiciones de las líneas y concluir que las líneas más grandes se encuentran cerca del centro, lo que tiene sentido porque es ahí donde está el punto más bajo. Por otro lado, las líneas más pequeñas se encuentran en el centro y en las esquinas porque es ahí donde, según la gráfica, la superficie es más plana.
2. 2. La dirección siempre es hacia el punto máximo más cercano: Como puedes observar en la imagen de la derecha, cada punto tiene su dirección hacia el siguiente punto que esta más alto.
   

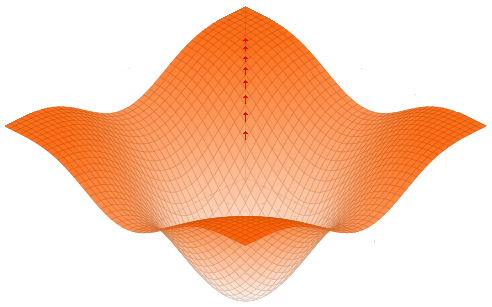
Algo muy interesante del gradiente es que, así como podemos ir hacia el punto más alto cercano siguiendo la dirección del gradiente, también podemos ir hacia el punto más bajo cercano siguiendo la dirección contraria al gradiente.

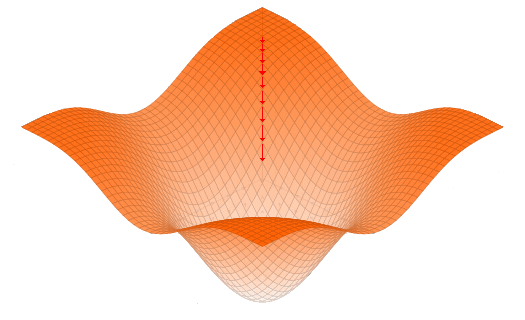
Para ponerlo más claro, si estamos parados en un punto cualquiera y tenemos un vector gradiente que va en la dirección x=2, y=2, es decir al punto más alto, para ir al punto más bajo deberíamos ir en la dirección contraria, es decir a x=-2, y=-2.

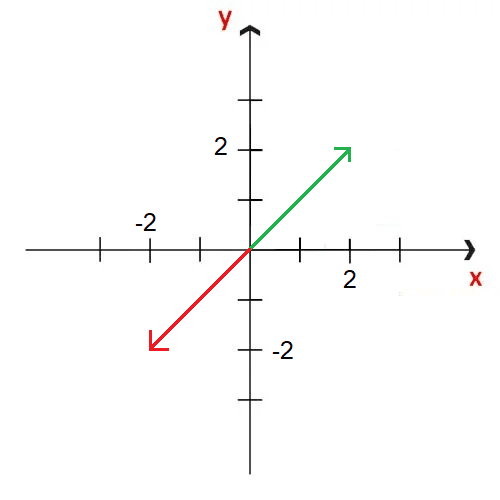
Entonces el gradiente es una herramienta matemática muy importante porque nos indica que dado cualquier punto en el cual nos situemos, podemos ir hacia el punto más alto cercano siguiendo la dirección del gradiente o podemos ir hacia el punto mínimo cercano siguiendo la dirección contraria al gradiente.

El Gradiente en Machine Learning

El gradiente juega un papel fundamental en el Machine Learning, especialmente en algoritmos de optimización que se utilizan para entrenar modelos. En muchos casos, el objetivo del aprendizaje automático es minimizar una función de pérdida que mide qué tan bien se está desempeñando un modelo en los datos de entrenamiento. El gradiente de esta función de pérdida con respecto a los parámetros del modelo indica la dirección en la que se deben ajustar los parámetros para reducir la pérdida. Los algoritmos de optimización, como el descenso del gradiente, utilizan esta información para actualizar iterativamente los parámetros del modelo hasta que se alcanza un mínimo o una convergencia satisfactoria.

Imagina que tienes la siguiente red neuronal de la siguiente forma:

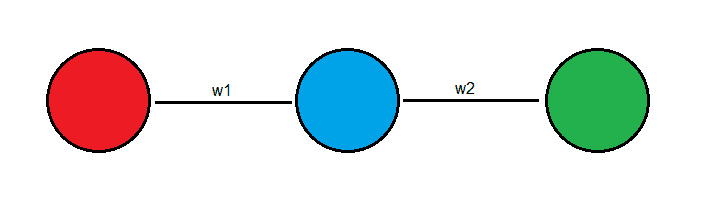
Esta red neuronal es una red simple que contiene 1 neurona de entrada, 1 neurona oculta y 1 neurona de salida, los cuales están conectados entre sí mediante pesos $w$. Lo que vamos a querer es que cuando le pasemos el numero 4 como entrada, nos devuelva un número, supongamos 1. Al principio los pesos serán aleatorios y el resultado que nos devolverá la red también será aleatorio. Es por eso por lo que deberemos entrenar la red. Entrenar la red implica ir cambiando los pesos hasta que nos devuelva las respuestas que queremos a partir de las entradas que le demos. En mi caso voy a entrenar a la red para que cuando le ingrese el numero 4 me devuelva el numero 1.

¿Y cómo medimos que tan lejos está el resultado que nos entrega la red del que nosotros queremos? Usaremos una función de perdida. Esta comparara el resultado obtenido de la red por el resultado que nosotros sabemos que es correcto y nos devolverá una medida de cuan errado esta este resultado. Por ejemplo, si le ingresamos a la red neuronal el numero 4 y nos devuelve un 6, cuando en realidad queremos que nos devuelva 1, el error se calculará así: $Error=Resultado_{Obtenido}-Resultado_{Correcto}$ es decir $Error=6-1$, lo cual es 5.

Básicamente de eso se trata entrenar redes neuronales: ir cambiando los pesos de la red para que, de acuerdo con una entrada determinada, nos devuelva una salida determinada.

Pero... ¿Que tiene que ver todo esto con el gradiente? Todas las interacciones entre los pesos y las neuronas desde las neuronas de entrada hasta las de salida representan funciones matemáticas y todas estas funciones combinadas representan una función matemática multivariable. Es decir que en el fondo nuestra red neuronal es solo una función multivariable más compleja y por eso podemos usar el gradiente para disminuir el error.

Descenso del Gradiente

El descenso del gradiente es un proceso matemático que implica calcular cuánta responsabilidad de ese error corresponde a cada uno de los pesos de la red neuronal. Luego, calculamos el gradiente de cada una de las neuronas y actualizamos los pesos de la red en la dirección contraria a la direccion gradiente.

Pero... ¿Porque debemos actualizar los pesos en la dirección contraria? Imagina que graficáramos todos los pesos de la función todos los pesos de la red en función del error final y al hacerlo obtuviéramos esta gráfica:

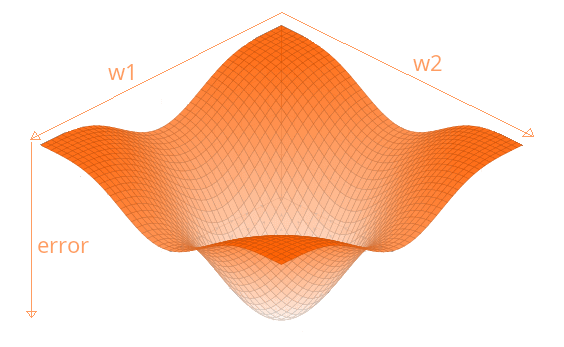
Como puedes observar en la función, al graficar los pesos obtendríamos el error en función de $w1$y $w2$. El error depende directamente de los pesos de la red neuronal.

Antes de seguir debo aclarar algo. Esta grafica que te muestro es solo una representación para poder ilustrarte como actúa el gradiente de una manera simplificada. En la realidad nuestra red neuronal va a tener cientos o miles de parámetros $w$, por lo que en la practica una función con más de parámetros, significaría una función con más de 3 ejes (recordemos que el error tambien es un eje) y por lo tanto no podríamos representarla gráficamente. Dicho esto, continuemos...

Si viéramos esta grafica desde arriba, obtendríamos esto:

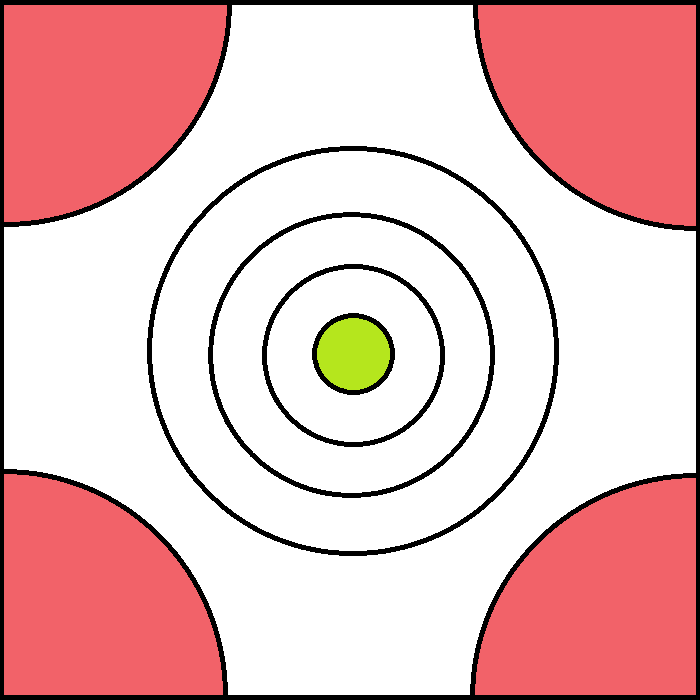
Las líneas en este cuadro sirven para delimitar alturas. En las esquinas se encuentran los puntos más altos coloreados en rojo, y en el centro en la parte más baja se encuentra el punto más bajo coloreado en verde. Las zonas no coloreadas son las están entre medio de estas dos últimas. Ahora vamos a colocarle a nuestra red ejes para poder ubicar puntos.

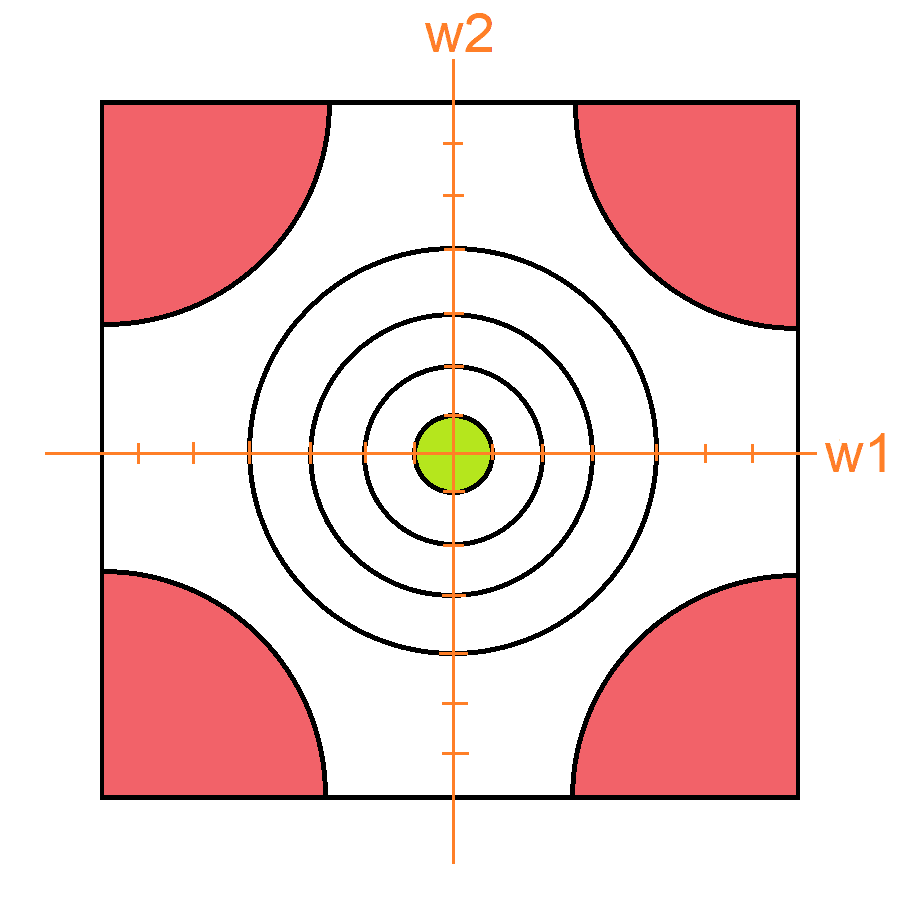
Los pesos de nuestra red van a estar inicializados como $w1=4$ y $w2=5$ por lo cual si ubicamos estos como un punto en nuestra grafica obtendríamos lo siguiente:

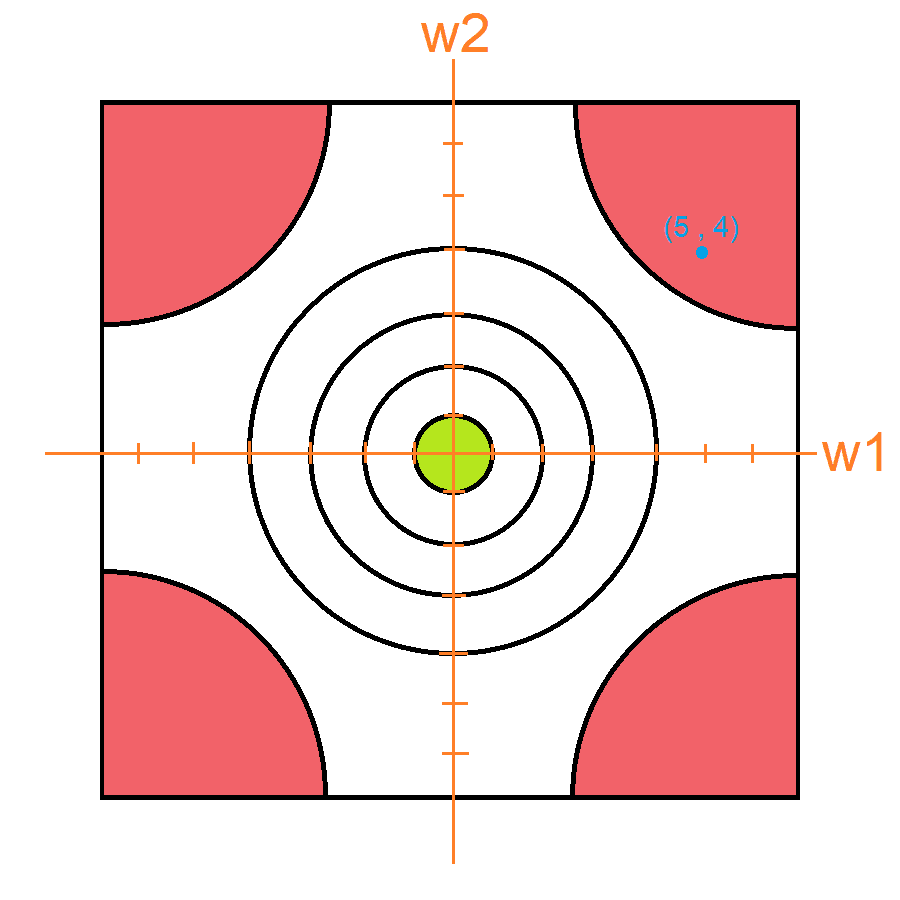
Mirando la gráfica podemos observar que nos encontramos en una zona donde el error es muy alto. Y lo que debemos hacer es bajar a la zona donde no lo es. Obviamente al verlo de manera grafica es muy fácil saber cómo modificar los pesos para que esto suceda, simplemente sumamos el vector $(-5,-4)$, lo cual nos dará lo siguiente:

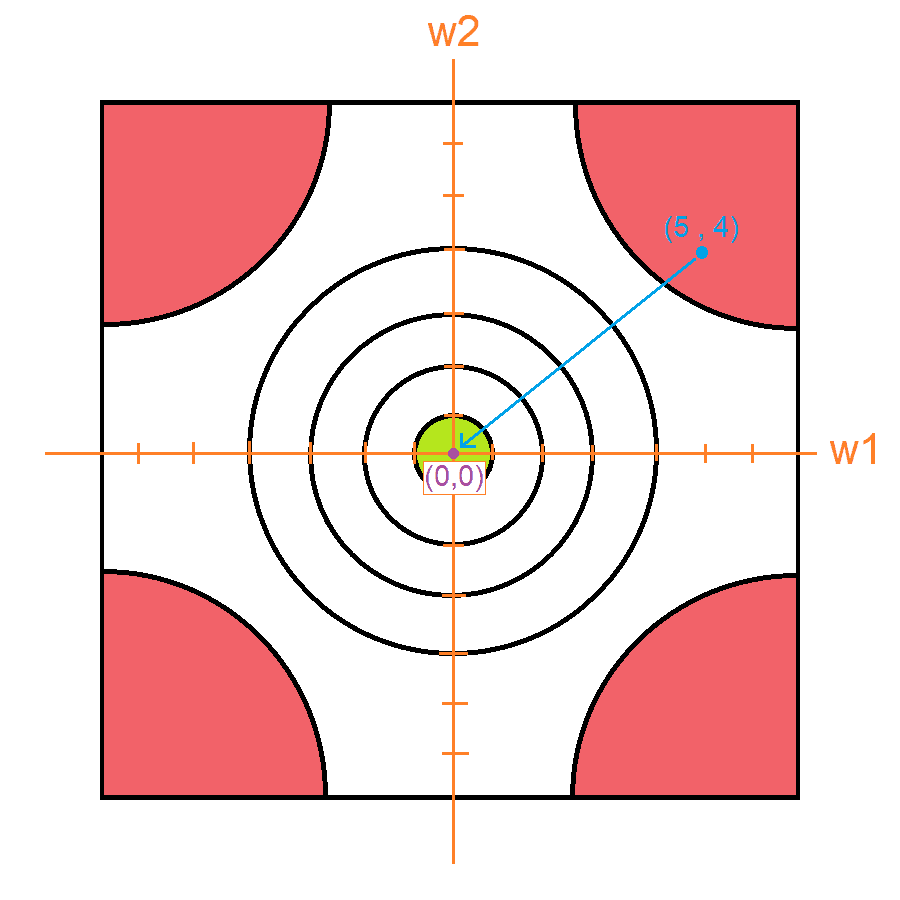
El problema es que como dije antes, las redes neuronales van a tener cientos o miles de parámetros, los cuales no se pueden graficar. Es aquí donde debemos calcular el gradiente. Suponte que yo calcule el gradiente y me dio el vector $(0.3, 0.6)$.

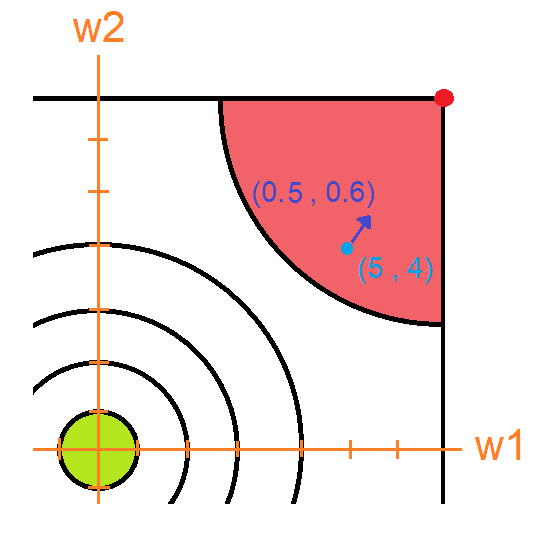
Este vector está apuntando al punto rojo que es el punto más alto cercano y es donde hay mayor error ¡Pero recordemos que lo que queremos es bajar el error, no subirlo! Por eso tomaremos siempre la dirección inversa al gradiente. Por eso a este proceso se le llama descenso del gradiente, porque usamos el gradiente para descender en nuestra gráfica de error.

Ahora que sabemos que debemos ir en dirección contraria, multiplicamos el vector gradiente por -1 quedando$(-0.5,-0.6)$ y lo sumamos con la posición actual $(5,4)+(-0.5,-0.6)=(4.5,3.4)$. De esta manera ya tenemos los nuevos valores de nuestra red neuronal: $w1=4.5$, $w2=3.4$

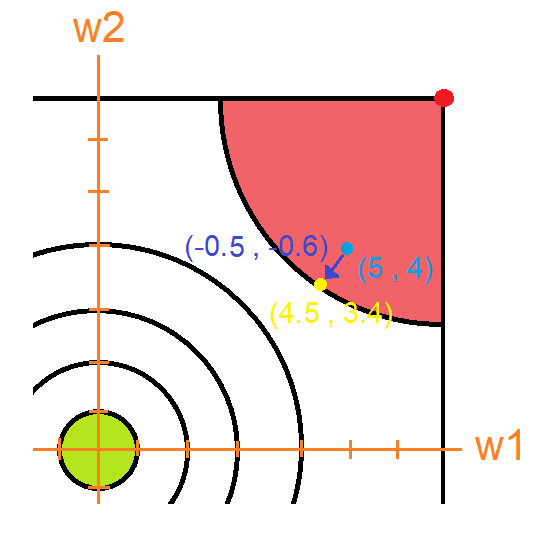
A cada una de estas actualizaciones en los pesos de la red neuronal se las conoce como 'pasos'. El paso que acabamos de hacer nos permitió bajar el error de la red neuronal. Si ingresamos de nuevo el numero 4 a nuestra red, terminaríamos obteniendo el numero 5.5 ¡Eso es una excelente señal! Nuestro nuevo resultado se acercó algo más a lo que queremos que sea 1. De hecho, si volviésemos a calcular el error obtendríamos esto: $Error=Resultado_{Obtenido}-Resultado_{Correcto}$ es decir $Error=5.5-1$, lo cual es $4.5$, menor a nuestro anterior error que era 5. Ósea que gracias a esa pequeña actualización en los pesos de la red neuronal logramos acercarnos un poco más a nuestro resultado deseado.

Sin embargo, esto no es suficiente. Por eso, para llegar a nuestro peso ideal deberemos realizar varios pasos, es decir,iterar el mismo proceso que hicimos hasta reducir el error a 0. Si lo hiciéramos, obtendríamos algo parecido a esto:

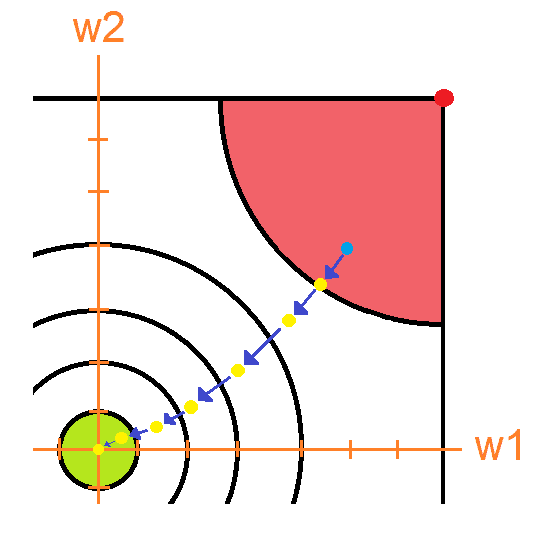
Una vez que hemos reducido el error hasta llegar a la zona verde, al ingresar el numero 4 a la red neuronal obtendremos nuestro valor deseado, es decir 1. Y si calculásemos el error obtendríamos esto $Error=1-1$ lo cual es cero. Que nuestro error sea cero indica que nuestra red se ha entrenado correctamente.

Antes de terminar me gustaría responder dos cuestiones: ¿Porque en la imagen los vectores gradientes son de diferentes tamaños? y tambien ¿Porque todos no son rectos al punto rojo que representa el punto más alto cercano?

Para empezar, debes recordar que la magnitud del gradiente cambia dependiendo de la inclinación del punto en la gráfica, lo cual explica porque los vectores son de diferente tamaño, como puedes observar en esta imagen:

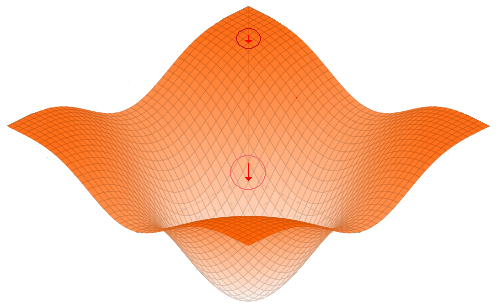
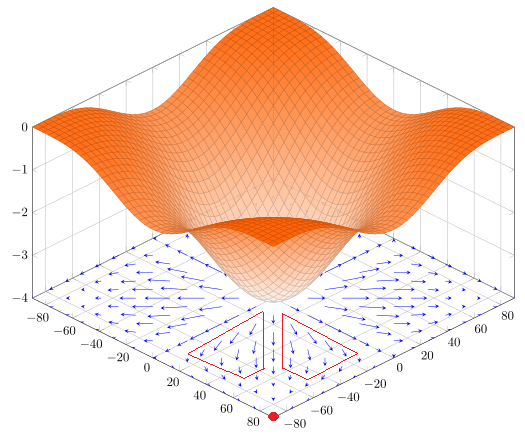
Por otro lado, el hecho de que los vectores no sean rectos al punto rojo tiene que ver con que, aunque el gradiente es siempre en la dirección de mayor cambio, dicha dirección va a variar dependiendo de la forma que tiene la función. En nuestro caso es una función muy irregular, por lo tanto, estas irregularidades pueden afectar la dirección ¡Pero no malentiendas! Si realizas el número suficiente de pasos el gradiente siempre te va a llevar al punto más alto.

De hecho, en la imagen que ilustra las direcciones del gradiente podemos observar como que, aunque los gradientes que se encuentran dentro de la zona marcada con una línea roja no apuntan directamente hacia la zona más alta cercana (punto rojo) sí que se van inclinando hacia dicha dirección hasta acercarse a él.

Trivia: Al momento de bajar el error en una red neuronal ¿Qué proceso se debe seguir?

Ascenso del gradiente

Descenso del gradiente

Multiplicación del gradiente

Dividir por cero el gradiente

Magnitud del gradiente

Al realizar un paso de optimización en la red neuronal, existe una forma de aumentar la posibilidad de este proceso. Debemos multiplicar el gradiente de cada paso que realicemos por un número que decidamos nosotros. Por ejemplo, imagina que en el ejemplo anterior multiplique todos los gradientes por 2. Lo que obtendría es una imagen como la siguiente:

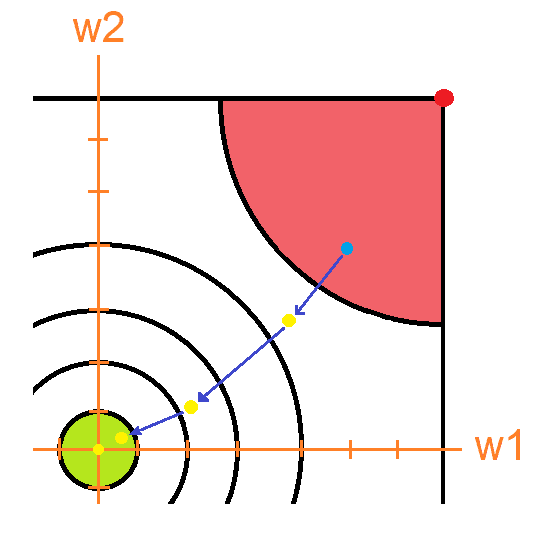
Este cambio fue muy bueno porque ahora logramos hacer optimizar los parámetros de nuestra red más rápido porque al ser el gradiente más grande, los cambios tambien sobre estos tambien lo son y por lo tanto nuestra red tarde 2 veces menos llegar a la zona de error baja (verde).

Pero lamentablemente no todo es color de rosas 🌹. Al multiplicar el gradiente por un numero hay que tener en cuenta dos cosas:

1. El gradiente resultante es muy grande: En este caso el problema erradica en que el gradiente jamás va a poder entrar a la zona verde porque la longitud de la zona.

   

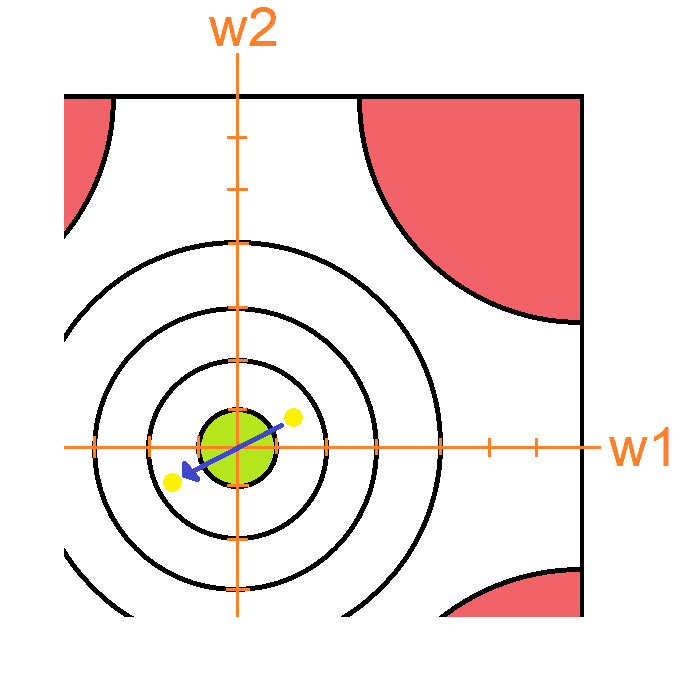
   En la imagen anterior pudiste ver que al ser el vector gradiente demasiado grande, este no se pudo adaptar al tamaño de la zona y por lo tanto termino sobrepasando. Si intentase ir a la zona verde desde el otro lado pasaría esto:

   

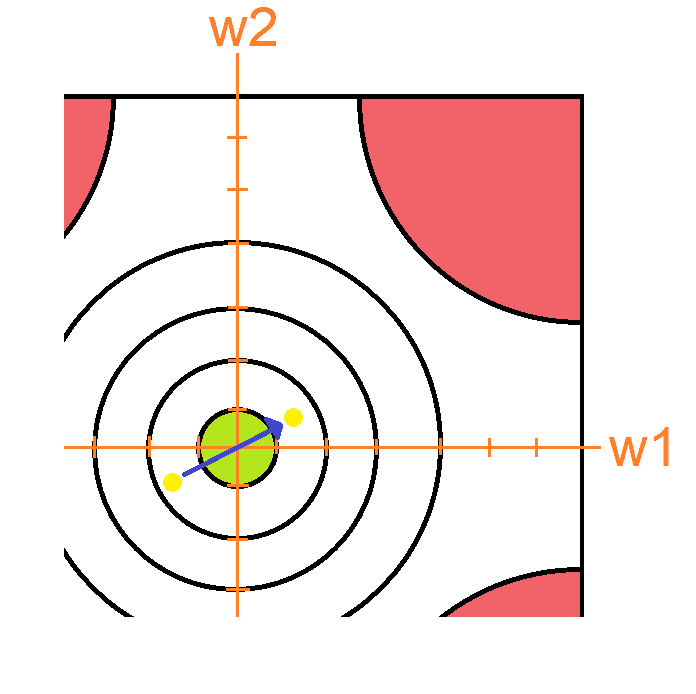
   Es riesgoso multiplicar el gradiente por un número muy alto porque puede provocar que los pesos de la red neuronal nunca entren en la zona verde de la gráfica y la red nunca nos devolverá un resultado satisfactorio.

2. *El gradiente resultante es muy pequeño: En este caso el problema es que tardaremos muchísimo en realizar la optimización de los parámetros porque los cambios a los pesos serán muy pequeños como se puede observar en la imagen:

   

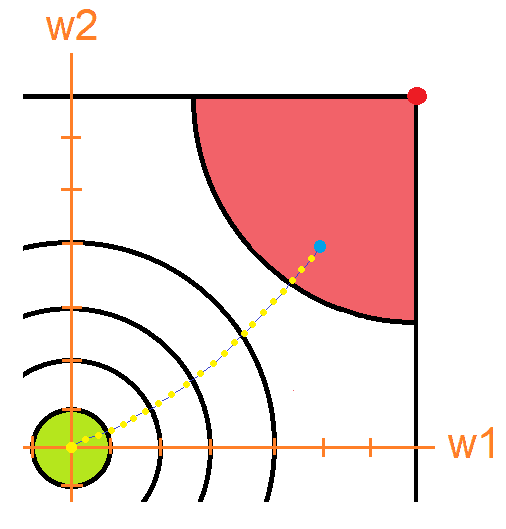
No hay una regla específica sobre que numero es mejor porque depende mucho de la arquitectura de la red neuronal y del problema y la verdadera solución es usar la vieja confiable: Ir probando hasta que funcione.

Conclusiones

El gradiente es un concepto matemático que llevado a la práctica se ha vuelto una base fundamental para el Machine Learning por su aplicación en la optimización de las redes neuronales, hasta tal punto que dichas redes le deben su popularidad a este algoritmo pues sin este no se podrían actualizar fácilmente y por lo tanto no tendríamos algunos de los mejores avances tecnológicos en este campo.

Sin embargo el gradiente no solo es utilizado en redes neuronales, sino tambien en otras partes como por ejemplo Regresión lineal y logística, Arboles de Decisión, Máquinas de vectores de soporte, etc., lo cual lo vuelve un elemento indispensable para aprender si deseas saber más sobre Machine Learning.

Hemos llegado al final de este artículo. Espero que te halla resultado útil y que hallas disfrutado leyéndolo tanto como yo disfrute escribiéndolo 😁.