'Trust Region Policy Optimization' o 'Optimización de Política mediante Región de confianza' (En español es más largo) es un método que se basa en actualizar los parámetros del modelo en cada paso tanto como sea posible, pero siempre dentro de un límite, el cual se le denomina región de confianza y como puedes intuir, de ahí viene el nombre del método.

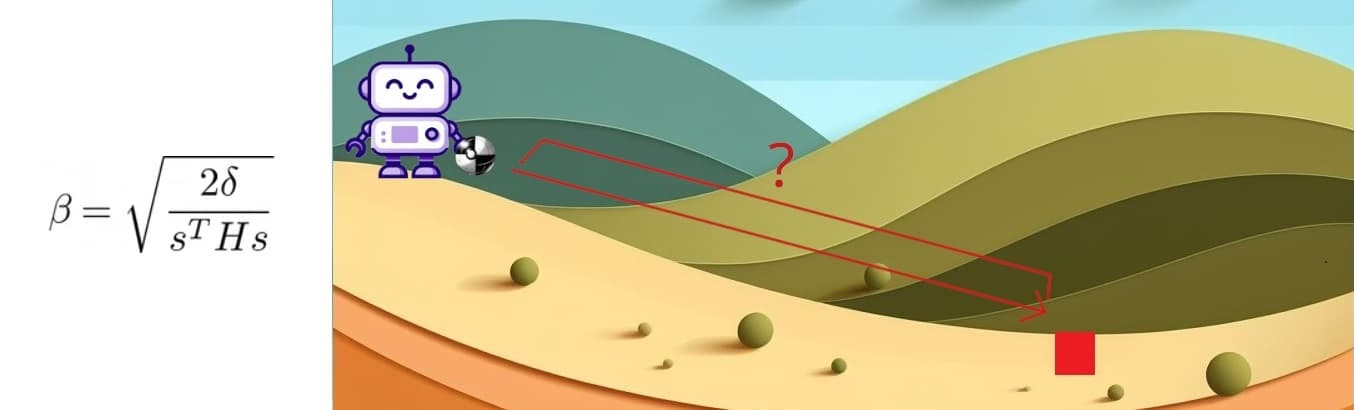
Veámoslo con un ejemplo. Supongamos que tengo que tirar una pelota desde la altura de una montaña y que tiene que caer dentro de un pozo rojo.

Pero al hacerlo nos encontramos con un problema 😞. Durante la caída, la pelota toma demasiada velocidad y se salta el pozo rojo siguiendo su rumbo hacia la nada misma. Adiós pelotita, que la fuerza te acompañe.

Para resolver este problema a alguien se le ocurrió que sería una buena idea poner un muro. De esta forma, aunque la pelota valla a gran velocidad, su trayectoria va a ser parada por ese muro. Pero recuerda que la pelota no solo debe parar, sino que también debe entrar en el pozo. Es por eso que pondremos el muro justo adelante del pozo.

¿Te diste cuenta? acabamos de restringir el movimiento de la pelota a la zona que sabemos que nos favorece. Si se queda a mitad de camino terminara cayendo corriéndose hacia el poso por que la pendiente de la colina es a favor de la dirección del pozo y si intenta irse de largo no va a poder porque está el muro.

Este ejemplo es una analogía que simplifica el funcionamiento de TRPO. Como explique antes, en TRPO se realiza una actualización de los parámetros (representados por la pelota blanca y negra) lo más grande posible (representado por el pozo rojo) pero con un límite (representado por el muro) porque de lo contrario esto se podría volver en contra y provocar un empeoramiento del rendimiento del modelo.

Es momento de ir a las matemáticas que fundamentan este procedimiento. Mira esta ecuación:

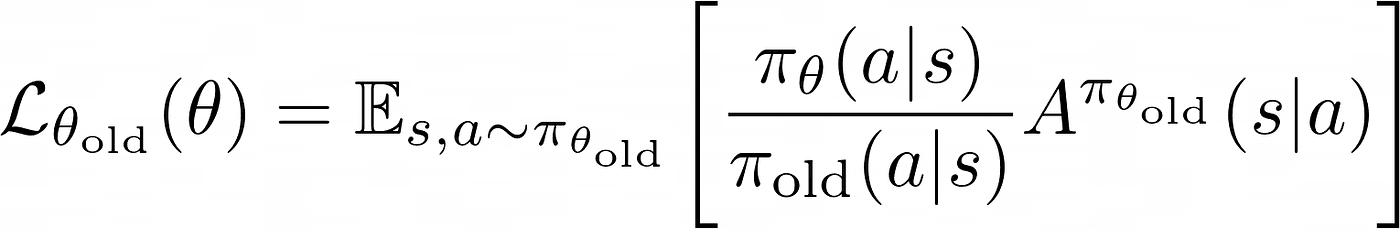
Siendo:

1. 1. $\frac{π_{θ}(a|s)}{π_{old}(a|s)}$: Esta fracción representa la proporción de probabilidad de seleccionar la acción $a$ dado el estado $s$ bajo la política con los nuevos parámetros $θ$ en comparación con la política anterior con parámetros $θ_{old}$. Esta proporción sirve como un indicador de cuánto ha cambiado la probabilidad de seleccionar una acción bajo la política actualizada en comparación con la política anterior.

2. 2. $A_{old}(a|s)$: Esta es una estimación de la ventaja de tomar la acción $a$ en el estado $s$ bajo la política anterior. La función de ventaja $A_{old}(a|s)$ mide cuánto mejor es tomar una acción en comparación con otras acciones en un estado dado bajo la política anterior.

Multiplicar estas dos partes juntas proporciona una estimación de cuánto deberíamos actualizar los parámetros de la política en un estado dado $s$ y una acción $a$. Si la proporción $\frac{π_{θ}(a|s)}{π_{old}(a|s)}$ es grande y la ventaja $A_{old}(a|s)$ es positiva, entonces esta acción debería ser más probable bajo la nueva política, y viceversa.

Esta ecuación representa la recompensa estimada. Como la recompensa es un buen indicador del rendimiento del modelo, queremos que nuestra recompensa sea cada vez mayor, por lo que debemos dedicarnos a encontrar cómo cada vez evaluado el modelo, esta funciona arroje un resultado mayor. Es decir que debemos maximizar esta función, pero sin sobrepasar un límite que hemos propuesto de manera arbitraria (región de confianza). En términos matemáticos se puede representar de esta manera:

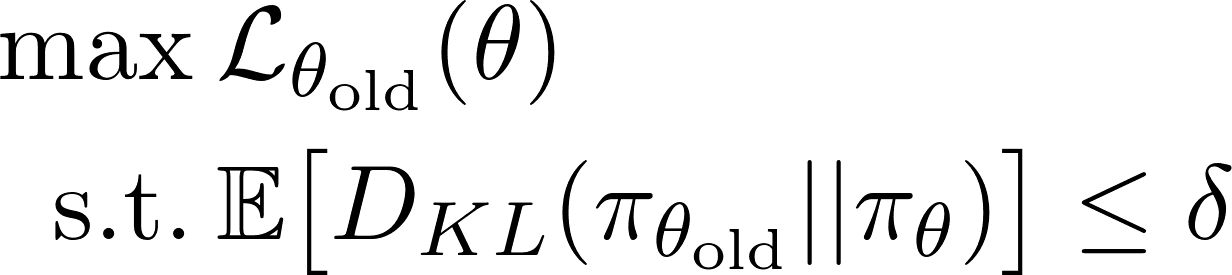
Esto significa: 'Maximizar la función de recompensa L siempre y cuando el termino Kl sea menor a δ', siendo δ un numero arbitrario, como por ejemplo 0.05. Pero... ¿Que es KL? KL es la 'Divergencia de Kullback-Leibler' y básicamente representa la diferencia entre dos probabilidades. Como puedes intuir, la manera que tendremos de medir que tanto se aleja la predicción del modelo con la política vieja en contraste con la política nueva es mediante el calculo de Kullback-Leibler entre las distribuciones de probabilidad viejas y nuevas.

Para ilustrarlo mejor, imagina que Aifa este ahora mismo sosteniendo la pelota y que la posición de la pelota representa los parámetros del modelo, es decir la política vieja:

Luego decide tirar la pelota hasta que esta se queda parada en algún punto.

En ese caso se podría decir que si la pelota cambio de posición, también lo hizo los parámetros del modelo, por lo tanto, ahora tiene una política nueva. Pues entonces en este caso podríamos decir que la divergencia de Kullback-Leibler es la distancia que recorrió desde la posición inicial, en la mano de Aifa, hasta la posición final, en el suelo de la colina.

¿Como maximizaremos la función?

Es cierto que tenemos la ecuación sobre la que tenemos que trabajar, sin embargo, es poco práctico hacerlo sobre esta en la forma la que está, por lo tanto, en vez de maximizar esta función, maximizaremos su 'Aproximación Polinomial de Taylor'.

¿Qué es la expansión Taylor?

Esto tiene sentido porque sólo necesitamos aproximarnos a la ventaja sustituta localmente cerca de los parámetros de nuestra política actual y los polinomios de Taylor son una muy buena herramienta para aproximar una función alrededor de un punto particular en algún intervalo usando solo términos polinomiales, que son mucho más fáciles de manejar en comparación con otras funciones. Entonces usamos la serie de Taylor para expandir la ventaja sustituta y el término de divergencia KL.

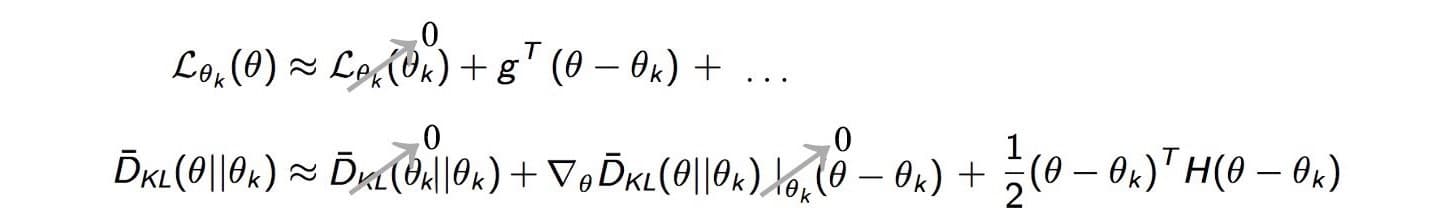
El primer término de L es 0, en cuanto a cambios de política pequeños, la distribución de los estados bajo las dos políticas es similar, la diferencia entre funciones de recompensa es cercana a L. Por lo tanto, para las mismas políticas es 0.

En el primer término de divergencia KL es 0 porque la divergencia entre las mismas distribuciones de políticas es 0. El segundo término es 0 porque si diferenciamos la ecuación de divergencia KL respecto a θ, cancelará la Integral y nos quedará:

Esto nos da el log (1) que es 0.

Finalmente, después de haber cancelado todos los términos pequeños nos queda lo siguiente:

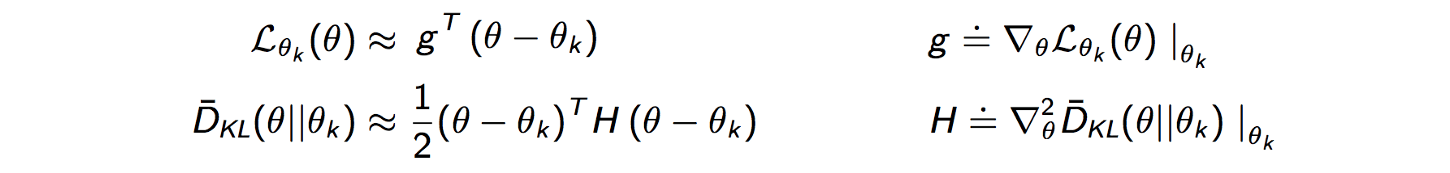
Ahora determinamos la dirección de búsqueda que va a maximizar nuestro objetivo. El termino $H$ con el termino $g$. La razón de esto es que$g$ representa en qué dirección hay mayor aumento de los cada uno de los parámetros del modelo. Y $H$ representa la 'intensidad' con la cual se deben cambiar los parámetros del modelo de acuerdo a Kullback-Leibler. Es decir que $g*H$ significaría 'Dirección del Cambio' por 'Intensidad del Cambio'. Sin embargo hay un problema 😞. Usar la matriz Hessiana directamente podría llevar a problemas, ya que esta matriz puede tener determinantes pequeños o incluso cero en ciertas direcciones, lo que complicaría la inversión de la matriz y podría resultar en pasos de actualización inestables o poco fiables. Al utilizar la inversa de la matriz Hessiana, se busca mitigar estos problemas. La inversa de la matriz Hessiana tiene la propiedad de 'compensar' las regiones donde la matriz Hessiana podría ser inestable o poco informativa. Además, al trabajar con la inversa, se logra controlar el tamaño del paso de manera más efectiva, ya que la inversa puede atenuar o amplificar la magnitud de las actualizaciones dependiendo de la curvatura local. Una vez definido esto, la ecuación nos queda de la siguiente manera:

¿Que representa esa H?

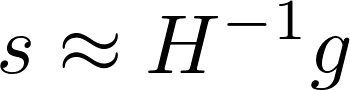
Y la magnitud del máximo paso posible se calcula con la siguiente ecuación:

Siendo:

1. 1. 2$δ$: Este término se refiere al doble del umbral de divergencia KL ($δ$). La divergencia KL es una medida de cuánto difiere la nueva política propuesta de la política actual. Multiplicar el umbral por 2 proporciona un margen adicional para asegurar que la nueva política no se aleje demasiado de la actual.

2. 2. $s^THs$: Aquí, $s$ es el vector que representa la dirección de búsqueda y $H$ es la matriz Hessiana de la función de costo. El producto $s^THs$ es esencialmente una medida de la curvatura de la función de costo a lo largo de la dirección de búsqueda. La matriz Hessiana captura cómo varían las segundas derivadas de la función de costo en diferentes direcciones. Por lo tanto, $s^THs$ cuantifica cómo cambia la función de costo en la dirección específica dada por $s$.

3. 3. $\sqrt{}$: La raíz cuadrada se aplica al cociente $\frac{2δ}{s^THs}$. Esto proporciona el factor de escala ($β$) que limita la magnitud de la actualización de la política. Tomar la raíz cuadrada asegura que el paso máximo se ajuste de manera proporcional a la relación entre el umbral de divergencia y la curvatura de la función de costo en la dirección de búsqueda.

Por lo tanto, es razonable pensar que el paso máximo posible va a ser igual a multiplicar la dirección hacia el punto óptimo, con la magnitud que necesitamos para llegar a dicho punto:

Ahora podemos recomponer esta ecuación sustituyendo los términos $s$ de esta manera:

Para ilustrarlo mejor considera lo siguiente: Esta ecuación representa cual es la dirección optima en la que Aifa debería lanzar la pelota.

Y esta representa cual el largo del recorrido en el cual Aifa debería hacer que la pelota se mueva.

Al multiplicar los dos factores anteriores obtenemos la dirección hacia la cual deberemos lanzar la pelota.

Con esto ya basta para calcular todas las actualizaciones de nuestro modelo. Sin embargo, hay un último problema a solucionar ¿Como calculamos la inversa de la matriz Hessiana?

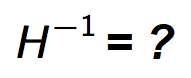
Calcular la inversa de la matriz Hessiana es muy costoso a nivel computacional, sobre todo para redes neuronales con muchos parámetros. Por si con esto no bastara, es numéricamente inestable. Así que de la misma manera que utilizamos la expansión de Taylor para aproximar función de ventaja sustituta, utilizaremos otro método para aproximar el cálculo. Para realizar esta aproximación utilizaremos el Gradiente Conjugado como método de aproximación ¿Recuerdas esta ecuación?

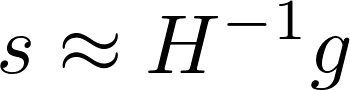
Pues resulta que si acomodamos el termino $H$ podemos verlo de la siguiente manera:

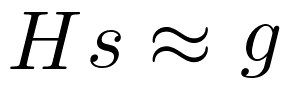
Si observas con atención notaras que la fórmula que nos quedo es muy parecida a una ecuación cuadrática:

Si es una ecuación cuadrática significa que esto se convierte en un problema de optimización cuadrática y por lo tanto podemos resolverlo mediante el método de Gradiente Conjugado.

¿Que es el metodo del Gradiente Conjugado?

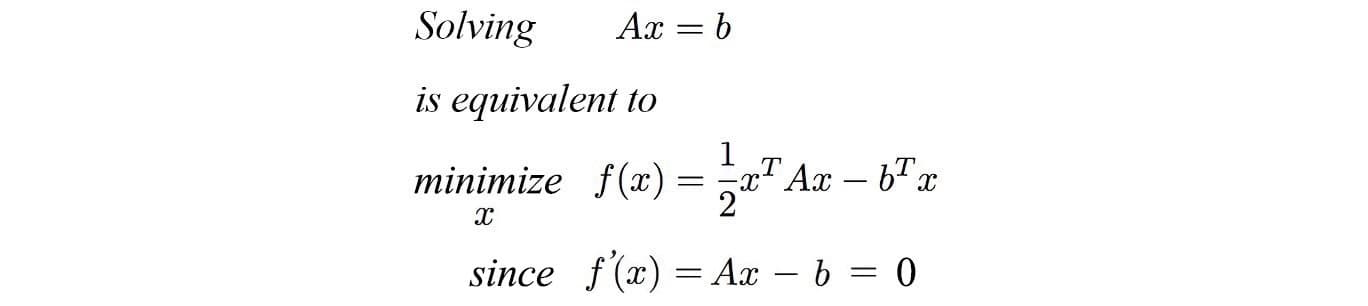
Lo cual se resuelve para la siguiente ecuación:

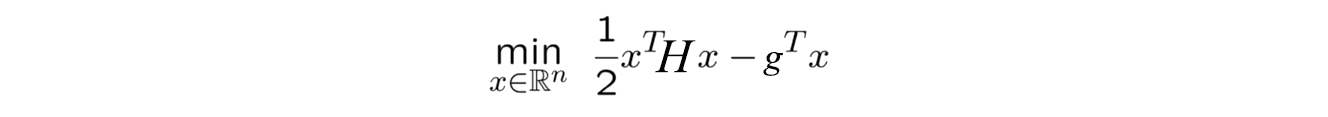
Line Search

Hemos realizado varias aproximaciones para hacer más afrontables las ecuaciones presentadas. Hemos usado tanto Taylor para realizar aproximaciones para maximizar la función de recompensa L como Conjugado del Gradiente para calcular la inversa de la matriz Hessiana. El problema es que todas estas aproximaciones pueden introducir errores. Entonces para resolver esto utilizaremos algo conocido como Line Search (Búsqueda por Línea).

El método Line Search funciona de la siguiente manera: Calculamos el valor de los nuevos parámetros del modelo de acuerdo a la siguiente formula (y teniendo en cuenta todas las aproximaciones preestablecidas):

Luego verificamos los parámetros de la nueva política teniendo en cuenta dos cosas:

1. 1. La divergencia de KL entre las políticas es menor que $δ$ (valor máximo permitido según la región de confianza).

2. 2. La ventaja sustituta $L$ es mayor o igual a 0 ($L$ está cerca de la diferencia entre la función de recompensa de dos políticas para pequeños cambios de política).

Introducimos un factor de decaimiento:

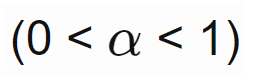
Si el paso actual no satisface las dos condiciones, lo debilitamos en un factor de $α$ y luego verificamos nuevamente las dos condiciones de esta manera:

Continuamos esto hasta que cumpla con las condiciones y luego usamos ese paso para realizar una actualización del parámetro de política θ. Es decir, si por ejemplo ahora siguiera sin cumplir las condiciones lo probaríamos multiplicándolo de nuevo por $α$:

Al hacerlo, damos el mayor paso posible para cambiar el parámetro de política θ de modo que no perjudique el rendimiento. Esto garantiza que encontremos el punto óptimo en nuestra región de confianza y luego continuemos desde allí.

Veamos un ejemplo usando Line Search

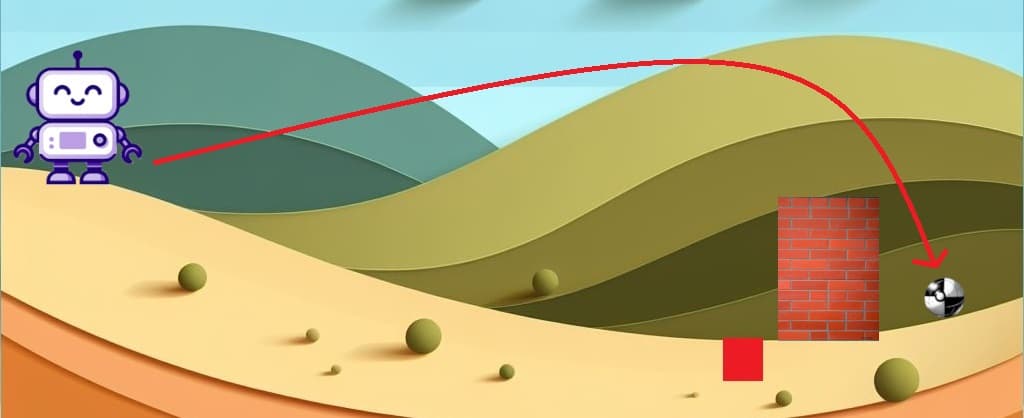
Supongamos que nuestro amigo Aifa decide tirar la pelota trazando una parábola con el fin de meterla en el pozo rojo. Pero lo que termina sucediendo es que la pelota cae adelante del muro. Esto es un error muy grande porque ahora la pelota no va a poder ingresar al pozo de ninguna manera y encima no la va a poder recuperar 😥:

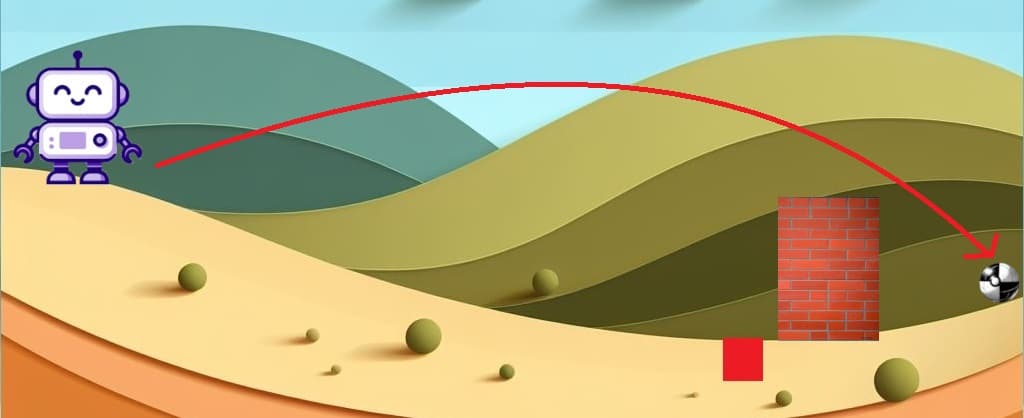
Según Line Search, cada vez que lanzamos la pelota tenemos que revisar dos cosas:

1. 1. La divergencia de KL entre las políticas es menor que $δ$.

2. 2. La ventaja sustituta $L$ es mayor o igual a 0.

Podríamos decir que la distancia que recorre desde la mano de Aifa hasta la posición detrás del adelante del muro representaría la divergencia de Kullback-Leibler (KL) y $δ$ representa el muro. Por lo tanto, no cumpliría este requisito porque la distancia entre la mano de Aifa y la pelota es mayor que la que hay entre la mano de Aifa y el muro ❌. Y, por otro lado, la ventaja sustituta $L$ estaría representada por la recompensa que representa la posición en la que quedo la pelota. Podríamos decir que la posición que hay detrás del muro la recompensa es positiva y si esta delante del muro es negativa porque es la posición que menos nos favorece debido a que no vamos a poder recuperar la pelota. Entonces tampoco cumple la segunda condición porque la ventaja sustituta L es menor a 0 ❌.

Lo que vamos a hacer entonces es reiniciar la situación y volver a tirar la pelota, pero disminuyendo la fuerza que usamos. Suponiendo que Aifa tiro la pelota con una fuerza de 1 Newton, vamos a multiplicarla por 0 < α < 1. Para efectos prácticos supongamos que$α$ = 0.95 para calcular la nueva fuerza. Entonces 'Fuerza * α' (1 * 0.95) es igual a 0.95. Entonces vamos a retratar la misma situación, pero corrigiendo modificando la fuerza a 0.95 Newtons.

Como puedes observar en la imagen de arriba, al repetir la misma situación, pero con menor fuerza dio un resultado parecido al primero, pero más cercano al objetivo de poner la pelota en el pozo. Por lo tanto, ahora vamos a volver a reiniciar la situación, pero probaremos multiplicando la fuerza por $α$ = 0.80, es decir (1 * 0.80). Esto significa que Aifa va a arrojar la pelota con una fuerza de 0.80 Newtons.

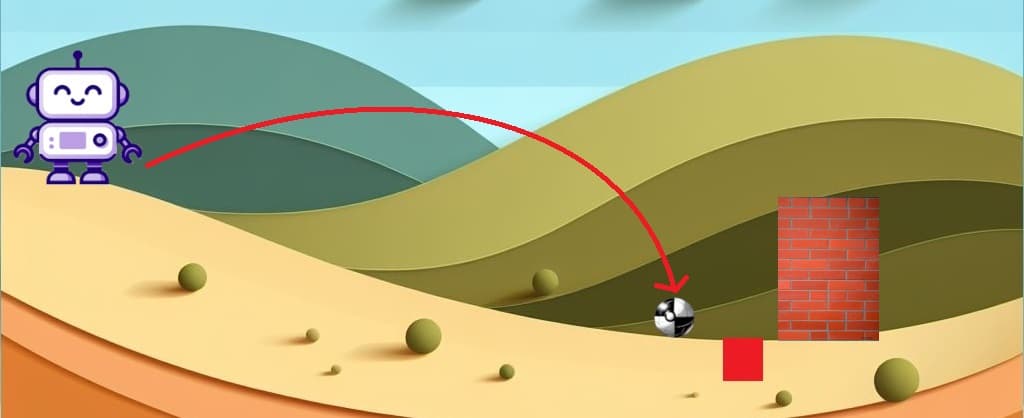
Al arrojar la pelota con la nueva fuerza obtenemos que la pelota queda parada a centímetros del pozo. Analicemos la situación en términos de las condiciones de Line Search:

1. 1. ¿La divergencia de KL entre las políticas es menor que $δ$? Dado que en este ejemplo el límite $δ$ está representado por el muro y la pelota no sobrepaso el muro, podemos decir que la divergencia KL es menor ✔️.

2. 2. ¿La ventaja sustituta $L$ es mayor o igual a 0? Si la pelota cae adelante del muro, es decir fuera de la zona entre Aifa y el pozo entonces la recompensa es negativa porque la pelota ya no se puede sacar de ahí. Pero si la pelota cae en la zona entre el muro y Aifa entonces es positiva porque podemos volver a agarrarla para volver a dar otro tiro ✔️.

Debido a que esta vez si se cumplen las dos condiciones, se podría decir que terminamos entrenar a Aifa, de tal manera que ha aprendido que para realizar un tiro óptimo debe usar una fuerza de 0.80 Newtons aplicando el método Line Search.

Quizás ahora te estes pregunta ¿Qué sentido tiene haber aprendido a tirar la pelota con una fuerza de 0.80 Newtons si no le dio en el pozo? Lo cierto es que tanto en este ejemplo como en TRPO en general, no se busca que aprenda a lanzar la pelota de manera perfecta en solo aplicando Line Search una vez. En un ejemplo de un entrenamiento real, el modelo va a ir entrenándose y aplicando Line Search todas las veces que sean necesarias hasta que logre tener el puntaje más alto posible. Volviendo con el ejemplo de Aifa, quizás si se aplicara Line Search 100 veces más será capaz de realizar el tiro al primer intento.

En resumen, Line Search se trata de buscar una actualización mediante varias iteraciones, reduciendo la intensidad del cambio en cada iteración por una constate $α$ (En el ejemplo de Aifa no era una constante, pero en ejemplos reales si lo es) con el fin de poder encontrar un punto en el que cumpla las condiciones necesarias para realizar una actualización que mejore el rendimiento del modelo.

Conclusiones

Trust Region Policy Optimization es un método que brinda estabilidad al entrenamiento debido a que está basado en optimizaciones dentro de una región de confianza. Otra característica importante es que TRPO es capaz de manejar espacios de acción continuos y de alta dimensión de manera efectiva, lo cual es importante en aplicaciones del mundo real. Sin embargo, también debemos recordar que para realizar dichas optimizaciones debemos realizar varios cálculos que a pesar de las aproximaciones que podamos realizar, en su conjunto son costosas, lo cual hace que este método sea computacionalmente menos óptimo que otros como por ejemplo Proximal Policy Optimization.

Hemos llegado al final de este artículo. Espero que te halla resultado útil y que hallas disfrutado leyéndolo tanto como yo disfrute escribiéndolo 😁.